Mates En La Vida: Trabajo de Geometría

1. El triángulo

1.1 Propiedades y tipos de triángulos

El triángulo es un polígono de tres lados.

Propiedades:

1. Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.

a < b + c

a > b - c

2. La suma de los ángulos interiores de un triángulo es igual a 180°.

A + B + C =180º

3. Si un triángulo tiene dos lados iguales, sus ángulos opuestos también son iguales.

Tipos:

Los triángulos se clasifican en dos grandes grupos: según sus lados y según sus lados.
Según sus lados son:

Equiláteros → todos sus lados son iguales.

Isósceles → dos lados son iguales y uno es diferente.

Escalenos → todos sus lados son diferentes.

Según sus ángulos son:

Acutángulo → sus tres ángulos son agudos, es decir, miden menos de 90º.

Rectángulo → un ángulo mide 90º y los otros dos son agudos (< 90).

Obtuso → uno de sus ángulos mide más de 90º, y los otros son agudos.

1.2 Rectas y puntos notables en el triángulo

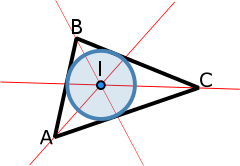
Incentro:
Es el punto central del triángulo, en el que todas las bisectrices coinciden.
A parte, es el centro de una circunferencia que está dibujada en el triángulo.

Baricentro:
Es el punto en el que coinciden las medianas del triángulo.
Una mediana: es el segmento que une un vértice con el punto medio del lado opuesto.

Resultado de imagen de imagen de un baricentro sin copyright

Circuncentro:
Es el centro de la circunferencia circunscrita del triángulo, también es el punto de intersección de las mediatrices del triángulo.
Una mediatriz: es la recta perpendicular a un lado que pasa por el punto medio del mismo.

Ortocentro:
Es el punto en el que coinciden las tres alturas del triángulo.
La altura: es el segmento que comienza desde un vértice y es perpendicular al lado opuesto a dicho vértice.

Este es un ejemplo muy práctico de los 4 puntos notables de un triángulo:

1.3 El Teorema de Pitágoras

Esta fue la frase que dijo Pitágoras, el gran filósofo y matemático, que marcó el mundo de las matemáticas:

Teorema de Pitágoras
En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Pitágoras

Este teorema fue comprobado por Pitágoras en el siglo VI a.C.
Lo que dice éste es que si queremos calcular la hipotenusa (a) de un triángulo rectángulo, lo único que tenemos que hacer es sumar los catetos al cuadrado cada uno (b y c) y hacer la raíz cuadrada de éstos.

a (al cuadrado) = b (al cuadrado) + c (al cuadrado)
a = raíz cuadrada de b (al cuadrado) + c (al cuadrado)

Un ejemplo:

Una curiosidad:
Se estima que otra persona lo haya descubrido antes de Pitágoras.

1.3.1 Demostración gráfica

1.3.2 El teorema en 3D

1.4 El teorema de Tales

Uno de los vídeos que explican muy bien, y con un toque cómico, es el vídeo de Les Luthiers - Teorema de Tales:

Y con este teorema...¿cómo podemos calcular la altura de un árbol a partir de su sombra?

¡Lo único que hay que hacer es una regla de tres!

Un ejemplo (según la imagen de abajo):
1,5 es a 2,25 como x es a 12. Si la resolvemos bien, daría como resultado 8 m.

2. Lugares geométricos

2.1 ¿Qué es un lugar geométrico?

Un lugar geométrico es un conjunto de puntos que cumplen determinadas condiciones o propiedades geométricas.

Algunos lugares geométricos son:

Circunferencia.
Elipse.
Parábola.
Hipérbola.

2.2 La mediatriz y la bisectriz

La mediatriz de un segmento es una línea recta, que es perpendicular a dicho segmento, trazada por su punto medio.
Otro nombre que tiene la mediatriz es simetral.

Siendo f la mediatriz:

La bisectriz de un ángulo es la semirrecta, que pasa por el vértice del ángulo y lo divide en dos partes iguales.

Las bisectrices de un triángulo coinciden en su incentro.

2.3 Las cónicas

2.3.1 ¿Qué es una cónica?

Una cónica es una curva plana, que surge a partir de las diferentes intersecciones entre un cono y el plano, es decir, es una curva obtenida al cortar el cono con un plano. El ángulo que forma el plano con el eje del cono, comparado con el ángulo que forman el eje y la generatriz del cono, determina las distintas clases de cónicas.
Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

2.3.2 La circunferencia

La circunferencia es el lugar geométrico de los puntos de un plano, que tienen la misma distancia a un punto. Es decir, que todos los puntos que forman la circunferencia, están a la misma distancia del centro.

Un ejemplo: La circunferencia es la Tierra.

2.3.3 La elipse

La elipse es un lugar geométrico de todos los puntos de un plano, cuya suma de las distancias a otros dos puntos fijos, llamados focos, es constante, es decir, que no varía.
Otra definición de elipse es que es una curva plana, simple y cerrada.
La elipse fue estudiada por Menecmo, investigada por Euclides, y su nombre se atribuye a Apolonio de Pérgamo.

Un ejemplo: La elipse es la trayectora de los planetas alrededor del Sol.

Obtención en un cono

Lo primero que debemos hacer es dibujar un círculo (nombre del centro; C) y un punto (A) en el interior del círculo. Después tenemos que dibujar un punto (B) y trazar la perpendicular a AB. El conjunto de dichas rectas envuelve a un elipse. Cuanto más cerca esté A de C, más parecida a una circunferencia será la elipse obtenida.

Método del jardinero

A este método se le denomina "del jardinero" porque sirve para trazar en el suelo elipses de gran tamaño y precisión suficiente, con medios modestos.

Lo que quiere decir el método del jardinero es que se atan los dos extremos de un hilo a dos chinchetas clavadas en los focos, y se mantiene el hilo tenso con un lapicero mientras vamos deslizándolo. La curva trazada corresponde con una elipse.

Mesa de billar elíptica

El billar elíptico se trata de una mesa de billar en la que las bandas rectas han sido sustituidas por una única banda contínua de forma elíptica. Es un dispositivo presente en algunos museos de ciencia que ya había fabricado, entre otras ideas ingeniosas, Lewis Carrol (autor de Alicia en el País de las Maravillas). Su característica principal es que cualquier bola lanzada desde un foco, o que pase por él, acaba pasando por el otro foco después de rebotar en la banda.

Imagen relacionada

2.3.4 La hipérbola

Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.

Es una sección cónica, una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.

Obtención en un cono

Lo primero que debemos hacer es dibuja un círculo (nombre del centro C) y un punto A exterior a la circunferencia. Se dibuja otro punto (Q) y se traza la perpendicular AQ. La familia de rectas obtenida es la envolvente de una hipérbola. Las perpendiculares C1 y C2 ,las circunferencias que pasan por A son las asíntotas de la hipérbola, rectas a las que la hipérbola se acerca en el infinito.

La lámpara hiperbólica

Muchas personas tienen en sus casas lámparas con pantalla, esas que normalmente se usan en las mesas de luz de las habitaciones, que al estar encedidas crean un cono de luz hacia arriba y otro hacia abajo, los cuales forman sobre la pared dos figuras con forma de hipérbole.

Las figuras sobre la pared, formadas por la luz de la lámpara, se pueden reproducir experimentalmente tomando las medidas de cualquier lámpara del tipo de lámpara que tengamos en casa y de su posición relativa a la pared.

Resultado de imagen de lampara hiperbolica

Resultado de imagen de lampara hiperbolica

2.3.5 La parábola

Una parábola es la sección cónica resultante de cortar un cono recto con un plano, cuyo ángulo de inclinación respecto al eje del cono sea igual al de su generatriz. El plano resultará paralelo a dicha recta. Se define también como el lugar geométrico de los puntos de un plano que equidistan (se ponen a la misma distancia) de una recta llamada directriz, y un punto exterior a ella llamado foco.

Aquí os dejo un ejemplo de las parábolas en la vida común:
Por ejemplo al botar un balón de baloncesto.

Obteción en un cono

Lo primero que debemos de hacer es dibujar una recta cualquiera (A) y un punto (X) no situado en ella. Desde cualquier punto (Z) de la recta, trazamos la perpendicular a XZ. La cantidad suficiente de rectas así construidas envuelven a una parábola con foco en el punto X.

La antena parabólica

La antena parabólica es un tipo de antena que se caracteriza por llevar un reflector parabólico, cuya superficie en realidad es un paraboloide de revolución.
Las antenas parabólicas pueden ser de tres tipos:

Transmisoras.
Receptoras.
Full dúplex.

El horno solar

El horno solar es una estructura que usa energía solar concentrada para producir altas temperaturas, usualmente para usos industriales. Reflectores parabólicos o helióstatos concentran la luz sobre un punto focal. La temperatura en este punto, puede alcanzar los 3500 °C, y este calor puede ser usado para generar electricidad, fundir acero, fabricar combustible de hidrógeno o nanomateriales...
El horno solar más grande es el horno solar de Odeillo, que está situado en Font-Romeu-Odeillo-Via, que se sitúan en Francia. Y fue inaugurado en 1970.

El espejo parabólico

Un espejo parabólico, es aquel que tiene una forma de antena parabólica, o cuyo perfil es similar a una parábola (y = x²).
Sus características son iguales a las de un espejo esférico.
Pero, a diferencia de éstos, un espejo parabólico tiene la particularidad, de que todos los rayos que llegan paralelos al eje óptico, se reflejan pasando por el foco.

3. Movimientos en el plano

3.1 Las traslaciones y ¿qué es un vector?

La traslación es un movimiento directo de uno o varios puntos, que mantienen la forma y el tamaño de las figuras.

Un vector es un elemento que transporta uno o varios puntos, de un lugar a otro. Sin cambiar su forma, tamaño...

3.2 Ejercicios de vectores y traslación

3.2.1 Dados los vectores u = (4, 3) y v (-1, 4), hallar:

a. Su representación gráfica en un sistema de coordenadas

b. los vectores u + v y u - v por la regla del paralelogramo

c. las componentes de los vectores anteriores

d. el módulo de cada uno de los vectores

3.2.2 Dibuja las figuras trasladadas de las siguientes en una traslación de vector guía u (4,3)

3.3 Giros

3.3.1 Ejercicio: Escribe la inicial de tu nombre y haz varios giros con ella.

3.4 Simetría ejercicios

3.4.1 Dado el triángulo de vértices A (-2, 2), B (6, -1) y C (7, 5) se pide:

a. Dibujar el triángulo

b. Hallar el triángulo simétrico respecto del centro de simetría O (0, 0)

c. Hallar el triángulo simétrico del eje OX

3.4.2 Euclides (aproximadamente 300 a. C.) enunció las leyes de reflexión de la luz sobre un espejo plano. Herón de Alejandría, 400 años después, afirmó algo más sencillo: "La luz ha de tomar siempre el camino más corto". Sirviéndote de esta idea, halla en que punto del espejo se ha de reflejar un rayo de luz que parte del punto A para que después llegue a B.

3.4.3 Carlos y Fernando están jugando al billar. En un determinado momento las bolas se encuentran en las posiciones indicadas por el dibujo. Indica el camino que debe seguir la bola A para que rebotando en la banda MQ golpee a la bola B.

Indica el camino que debe seguir la bola A para que rebotando en la banda NP y PQ golpee a la bola B.

3.4.4 Inventa un abecedario simétrico y escribe una frase

Frase: Me llamo Lucía

3.5 Frisos, mosaicos y cenefas

Frisos: El friso es el conjunto de molduras que coronan un edificio, situada entre el arquitrabe y la cornisa. Éste a su vez es una larga banda decorativa pintada, esculpida o caligrafiada.

Mosaicos: El mosaico es un conjunto de pequeñas piezas, llamadas teselas, que forman una obra decorativa.
La relación que tienen los mosaicos con las matemáticas es que las teselas forman figuras geométricas, simetrías,giros...
Por ejemplo, la imagen está formada por pentágonos rojos, azules y amarillos.

Cenefas: La cenefa es un mosaico construido mediante traslaciones de distintas figuras.

3.6 MC. Escher

MC. Esther fue un artista neerlandés, que nació en Leeuwarden, en los Países Bajos, el 17 de junio de 1898, y murió el 27 de marzo de 1972, en Hilversum, Países Bajos.

Este artista es conocido por sus grabados xilográficos, es decir, unos grabados que se realizaban con planchas de madera...

También es conocido por sus dibujos, que contienen figuras imposibles, teselados y varios mundos imaginarios.

Algunas obras de las más importantes de Escher son:

(Three Spheres II) Tres esferas II

(Waterfall) Cascada

(Relativity) Relatividad

4. Resumen de áreas y volúmenes de figuras conocidas

5. La esfera y el globo terráqueo

5.1 Elementos principales de la esfera

(estas partes pertenecen a la esfera, NO AL CÍRCULO)

Centro: es el punto en el que coincide cualquier línea que dibujes desde la esfera.

Radio: es la distancia que hay desde el centro a cualquier punto de la esfera. Es decir, es la mitad de la distancia del diámetro.

Cuerda: es el segmento que une dos puntos de la superficie.

Diámetro: es la cuerda que pasa por el centro.

Polos: son los puntos del eje de giro que quedan sobre la superficie esférica.

5.2 Elementos de la esfera terrestre

Los paralelos: son los círculos formados por la intersección entre la Tierra y un plano imaginario, perpendicular al eje de rotación de la Tierra.

Los meridianos: son los semicírculos que pasan por el Polo Norte y el Polo Sur.

5.3 Los husos horarios, la hora local solar y oficial.

El huso horario, en geografía, es cada una de las 24 áreas en que se divide la Tierra.
Se llaman así porque tienen forma de huso de hilar.
Todos los husos horarios se definen en relación con el denominado tiempo universal coordinado (UTC), huso horario centrado sobre el meridiano de Greenwich, también conocido como meridiano cero).

Un dato curioso es que hay que suma una hora, cuando la Tierra gira de oeste a este, y pasa de un huso horario a otro (en dirección este). Habría que restar una hora, cuando la Tierra girara de este a oeste.

5.4 El método de Eratóstenes para calcular el diámetro de la circunferencia terrestre

Un vídeo que puede ayudarte a comprender este punto es este:

Lo que hizo Erastótenes fue poner una estaca en un país (Siena) a una hora determinada para que no se formase su propia sombra.
Y también puso otra , en otro lugar (Alejandría), sitio en el que a esa hora hacía sombra.
Y con esos datos fue capaz de calcular el diámetro de la Tierra.

RETOS:

Te reto a que con el Teorema de Tales, averigues la altura que tendrá un árbol, sabiendo que su sombra es de 5m y una estaca, mide m y su sombra es de 3m.

También te reto a que sepas decirme la diferencia que hay entre un cilindro y un cono.
Te doy una pista muy grande, tiene que ver el volumen...

Bibliografía:

miércoles, 10 de mayo de 2017

Trabajo de Geometría